¿En qué planta acabará Alicia si coge el ascensor en la planta 3ª, sube 2 plantas y baja 7?
Evidentemente, Alicia terminará dos pisos por debajo de la planta que está a pie de calle. No existe ningún número natural que represente el piso donde acabará Alicia.
Un número por debajo del cero es un número negativo. En nuestro ejemplo, 2 por debajo del cero es -2.
El conjunto de los números enteros (Z) está compuesto por los números negativos y los números naturales.
Z = {... , -100, ..., -5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5, ..., +100, ...}
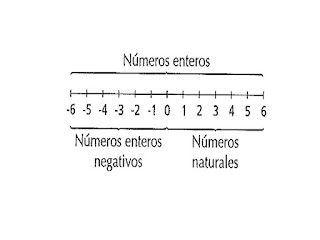
Representación de los números enteros en la recta
En la recta el cero marca el origen. A la izquierda del cero aparecerán los números enteros negativos y a la derecha del cero los números enteros positivos, es decir, los números naturales.
Opuesto de un número entero
Todo número entero tiene su opuesto, que se corresponde con el simétrico respecto del 0. Por ejemplo, el opuesto de -3 es 3 y el opuesto de 5 a -5.
Valor absoluto de un número entero
El valor absoluto de un número entero es el mismo número sin el signo. Por tanto, el valor absoluto de un número es siempre positivo:
- El valor absoluto de un número positivo es él mismo.
- El valor absoluto de un número negativo es su opuesto.
OPERACIONES CON NÚMEROS ENTEROS
Suma y resta de números enteros
Las reglas básicas para sumar y restar números enteros son las siguientes:
1. Para sumar dos números enteros del mismo signo se suman los valores absolutos de los números y se
deja el signo que tienen.
(+a) + (+b) = +(a + b) (-a) + (-b) = -(a + b)
2. Para sumar dos números enteros de distinto signo se restan los valores absolutos de los números y se deja el signo del que tenga mayor valor absoluto.
(+a) + (-b) = +(a - b) si
a > b
(+a) + (-b) = -(b - a) si
b > a
3. La resta de dos números enteros es la suma del primero más el opuesto del segundo.
(+a) - (+b) = (+a) + (-b) (+a) - (-b) = (+a) + (+b)
Producto de números enteros
Para multiplicar números enteros tenemos que:
1. Multiplicar los valores absolutos de los números.
2. Poner el signo resultante de aplicar la regla de los signos.
División de números enteros
Para dividir números enteros tenemos que:
1. Dividir los valores absolutos de los números.
2. Poner el signo resultante de aplicar la regla de los signos.
Operaciones combinadas
Tenemos operaciones combinadas cuando en una misma operación hay sumas, restas, multiplicaciones, divisiones y, a veces, paréntesis y corchetes. Para resolver estas operaciones aplicaremos el siguiente orden:
1. Lo primero que hay que resolver son las operaciones que aparecen dentro de los paréntesis y corchetes. Para calcular las operaciones que hay en su interior se aplican las reglas generales.
2. Se realizan los productos y las divisiones.
3. Si hay varios productos y divisiones encadenados se operan siguiendo el orden de izquierda a derecha.
4. Se realizan las sumas y las restas.
5. Si existen varias sumas o restas encadenadas se operan siguiendo el orden de izquierda a derecha.
Para repasar


No hay comentarios:
Publicar un comentario